[C++ / Algorithm] 백준 13306번 트리 #21

1. 트리

1-1. 문제

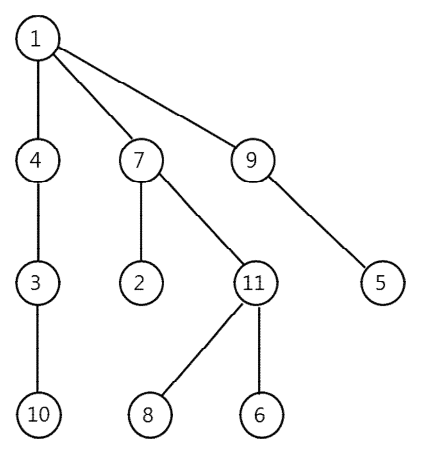
트리 T는 아래 그림 1과 같은 구조를 가지고 있으며 원은 ‘정점’이라 하고, 정점과 정점을 연결하는 선을 ‘에지’라 한다. 특히 가장 위에 위치한 정점을 ‘루트’라 하는데 오직 하나만 있다.
N개의 정점들은 숫자 1부터 N으로 표현하고 루트는 항상 1이다.

두 정점 v와 w를 연결하는 경로는 정점들의 순서리스트 (v0, v1, …, vm)로, 정점 vi와 vi+1은 에지로 연결되고 v0 = v, vm = w이다.
트리에서는 임의의 두 정점 v와 w 사이에 항상 두 정점을 연결하는 경로가 오직 하나만 존재한다.
예를 들어, 그림 1에서 정점 3과 11 사이의 유일한 경로는 (3, 4, 1, 7, 11)이다.

각 정점 v에서 루트 r과 연결하는 유일한 경로 P에 대해서 정점 v와 에지로 연결된 정점 중에서 P상에 있는 정점을 v의 ‘부모 정점’이라고 한다.
예를 들어, 그림 1에서 4, 7, 9의 부모 정점은 1이고, 2와 11의 부모 정점은 7이다.

트리 T에서 어떤 두 정점을 연결하는 에지를 제거하면 그 두 정점 외에도 경로가 존재하지 않는 정점 쌍이 있을 수 있다.
여러분은 “정점 v와 w를 연결하는 경로가 존재하는가?”와 같은 질의에 답해야 한다.
예를 들어, 그림 1에서 7과 11 사이의 에지를 제거하면 8과 5를 연결하는 경로는 존재하지 않는다.

트리 정보가 주어지고, 에지의 제거 정보와 질의가 임의의 순서로 주어질 때, 작업을 순서대로 수행하며 질의에 대한 답을 출력하는 프로그램을 작성하시오.

1-2. 입력

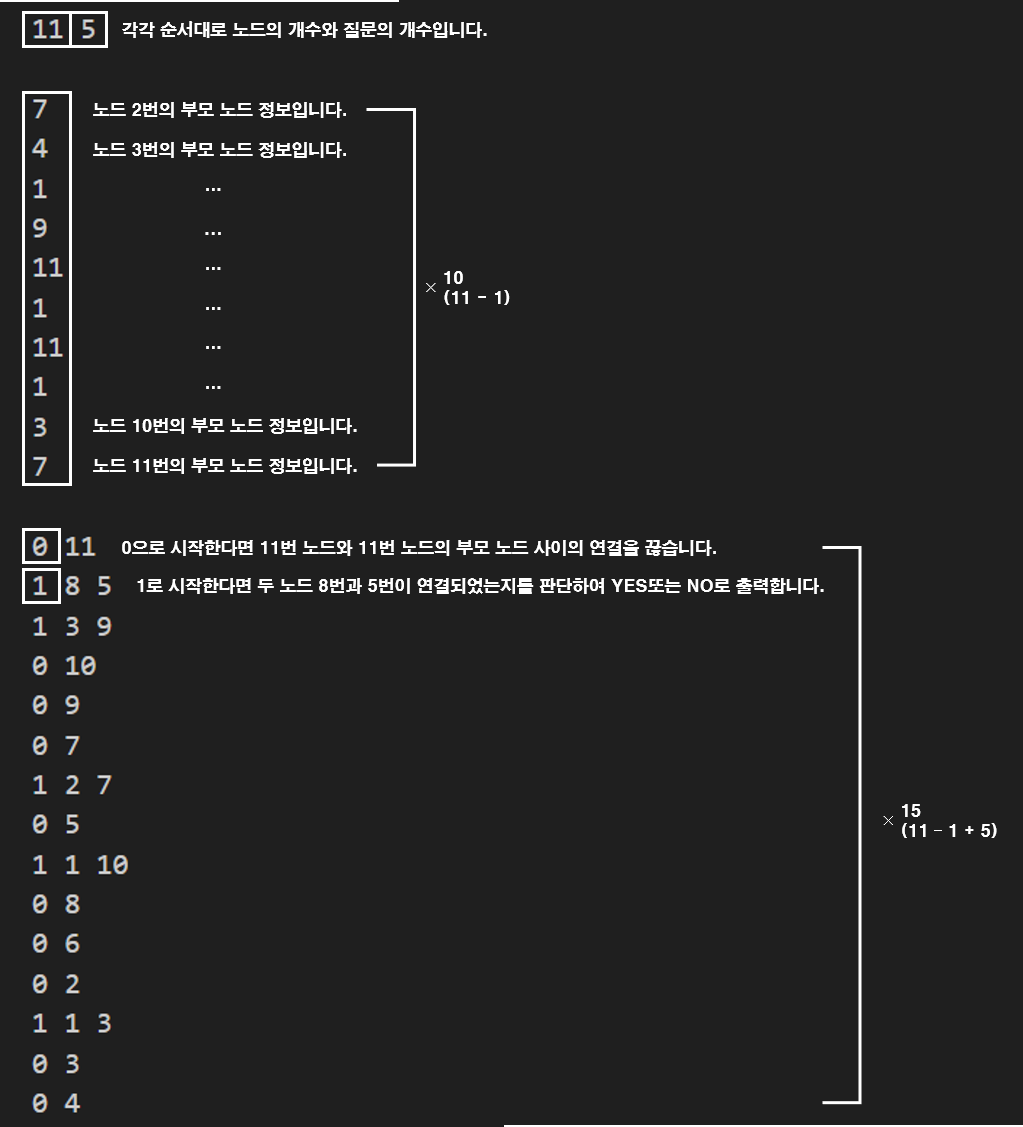
표준 입력으로 다음 정보가 주어진다. 첫 번째 줄에는 트리의 정점의 개수와 질의의 개수를 나타내는 두 정수 N과 Q (1 ≤ N, Q ≤ 200,000)가 주어진다.
다음 N-1개의 줄의 i번째 줄에는 정점 i+1의 부모 정점을 나타내는 정수 a가 주어진다 (1 ≤ a ≤ N).
다음 (N-1)+Q개의 줄 중에서 N-1개는 (1)의 형태로, Q개는 (2)의 형태로 주어진다.

• (1) 두 정수 x와 b가 주어진다(x = 0, 2 ≤ b ≤ N). 이것은 b의 부모 정점과 b를 연결하는 에지를 제거함을 의미한다. 각 줄의 b는 모두 다르다.
• (2) 세 정수 x, c, d가 주어진다 (x = 1, 1 ≤ c, d ≤ N). 이것은 c와 d를 연결하는 경로가 존재하는 지 묻는 질의를 의미한다.

2. 풀이

유니온 파인드는 간선을 추가하는 과정에서 사용할 수 있지만, 해당 문제를 준비된 간선들을 하나씩 지우며 확인하기 때문에 사용할 불가능해 보입니다. 하지만, 상태를 확인하는 모든 간선들을 끊어 놓은 상태로 해당 명령들을 스택에 저장한 후 거꾸로 꺼내면서 간선 삭제 명령을 간선 생성으로 만든다면 유니온 파인드를 사용할 수 있게됩니다.

#include <iostream>
#include <utility>
#include <stack>
#include <string>

using namespace std;

typedef pair<int, pair<int, int>> Query;

int numberOfNodes, numberOfQueries;
const int MaxLength = 200000 + 1;
int parents[MaxLength];
stack<Query> queries;
stack<string> answers;

int doFind(int x) { // 특정 노드가 속하는 그래프의 대표 요소를 반환합니다.
	if (x == parents[x]) return x;
	return parents[x] = doFind(parents[x]);
}

void doUnion(int x, int y) { // x가 속하는 그래프와 y가 속하는 그래프를 연결합니다.
	x = doFind(x); 
	y = doFind(y);

	if (x == y) return;

	parents[x] = y;
}

int main() {
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	cin >> numberOfNodes >> numberOfQueries;

	for (int node = 2; node <= numberOfNodes; node++) {
		int parent;

		cin >> parent;

		parents[node] = parent;
	}

	int numberOfTotalQueries = numberOfNodes + numberOfQueries - 1;

	while (numberOfTotalQueries--) {
		int queryType, from, to, targetNode;

		cin >> queryType;

		if (!queryType) {
			cin >> targetNode;

			queries.push({ 0, { targetNode, parents[targetNode] } });

			parents[targetNode] = targetNode;
		}
		else {
			cin >> from >> to;

			queries.push({ 1, { from, to } });
		}
	}

	while (!queries.empty()) {
        Query query = queries.top();

		if (query.first) {
			int from = query.second.first;
			int to = query.second.second;

			if (doFind(from) == doFind(to)) answers.push("YES");
			else answers.push("NO");
			
		}
		else {
			int targetNode = query.second.first;
			int parent = query.second.second;

			doUnion(targetNode, parent);
		}

		queries.pop();
	}

	while (!answers.empty()) {
		cout << answers.top() << "\n";

		answers.pop();
	}

	return 0;
}

11 5

7
4
1
9
11
1
11
1
3
7

0 11
1 8 5
1 3 9
0 10
0 9
0 7
1 2 7
0 5
1 1 10
0 8
0 6
0 2
1 1 3
0 3
0 4

NO
YES
YES
NO
YES