[C++ / Algorithm] 선분과 점 사이의 거리 #23

1. 선분과 점의 위치 관계 분석

이 문제는 선분 AB와 P의 위치관계를 분석해서 3가지의 예외상황으로 나누어 풀면 쉽습니다.

1. 점 P에서 선분 AB로 수선을 그릴 수 있을 때

2. 점 P에서 선분 AB로 수선을 그릴 수 없으며 점 P가 점 A랑 더 가까울 때

3. 점 P에서 선분 AB로 수선을 그릴 수 없으며 점 P가 점 B랑 더 가까울 때

이 3가지의 상황은 AP 벡터를 AB 벡터에 정사영시켜 구분할 수 있습니다.

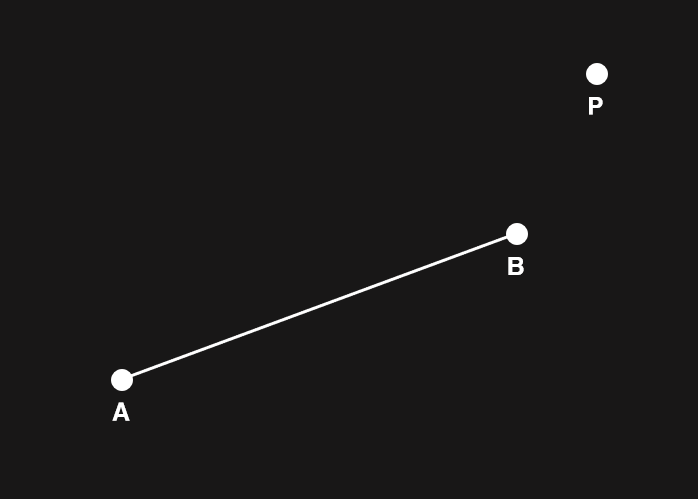
AP 벡터와 AB 벡터를 정사영시킨 벡터의 길이가 0 이하이라면 아래 그림과 같이 점 P는 선분 AB에 수선을 그을 수 없을 상태이며, 점 A와의 거리가 선분 AB와의 거리가 된다는 것을 알 수 있습니다.

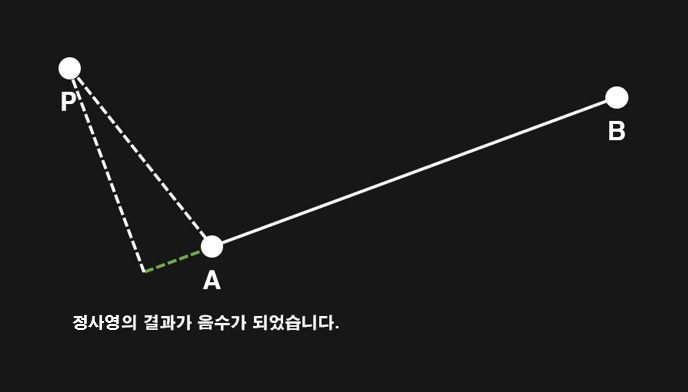
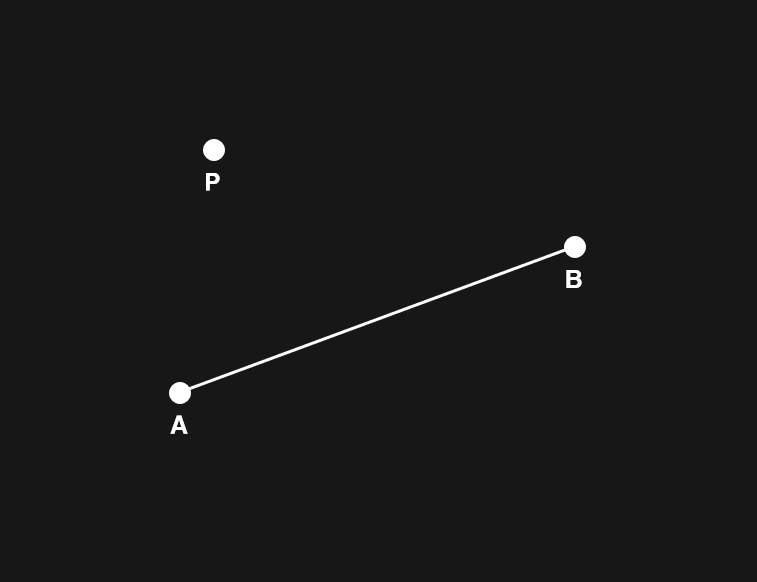
만약 길이가 선분 AB의 길이보다 작거나 같은 양수라면 아래 그림과 같이 선분 AB에 수선을 그려서 거리를 측정할 수 있습니다.

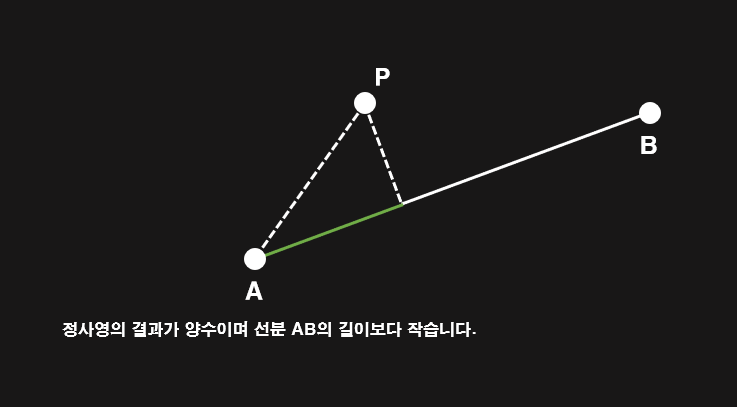
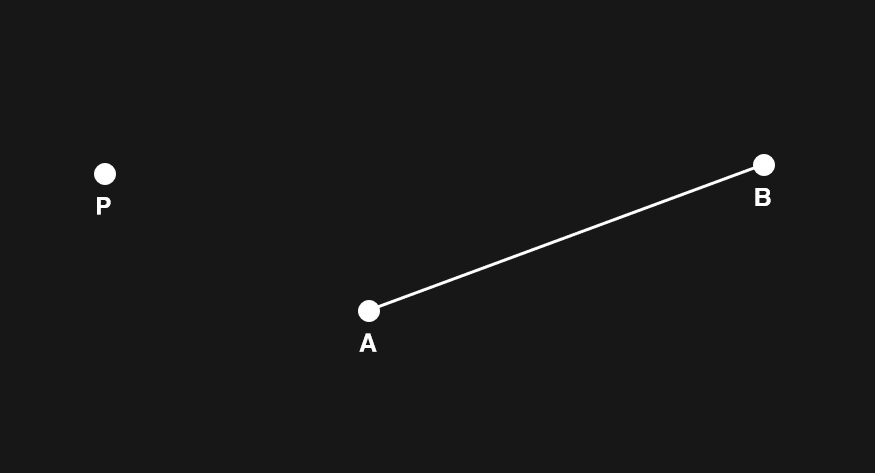
마지막으로 길이가 선분 AB의 길이보다 크다면 점 B와의 거리가 선분 AB와의 거리가 됩니다.

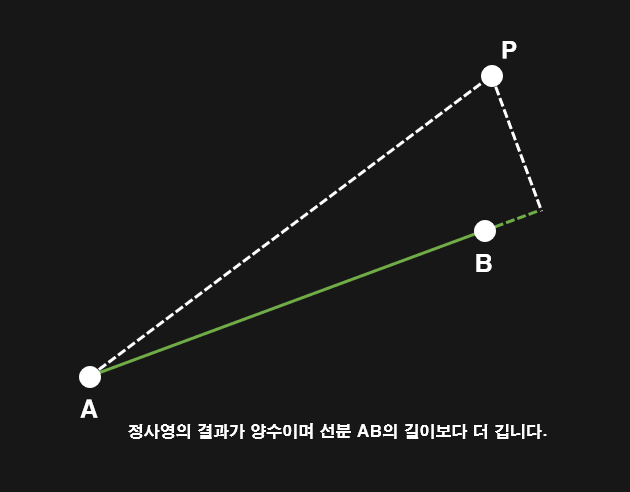
2. 코드

#include <iostream>
#include <cmath>

using namespace std;

struct Vector {
	double x;
	double y;
};

double length(Vector a) {
	return sqrt(a.x * a.x + a.y * a.y);
}

double getDistance(Vector a, Vector b) {
	double dx = b.x - a.x;
	double dy = b.y - a.y;
	return length({ dx, dy });
}

double dot(Vector a, Vector b) {
	return a.x * b.x + a.y * b.y;
}

double getSegmentDistance(Vector a, Vector b, Vector p) {
	Vector line = { b.x - a.x, b.y - a.y };
	double lineLength = length(line);

	if (lineLength == 0) return getDistance(a, p);

	double projection = dot({ p.x - a.x, p.y - a.y }, { b.x - a.x, b.y - a.y }) / lineLength;

	if (projection <= 0) return getDistance(a, p);
	else if (projection >= lineLength) return getDistance(b, p);
	else {

		Vector projectionVector = {
			a.x + line.x * projection / lineLength,
			a.y + line.y * projection / lineLength
		};

		return getDistance(projectionVector, p);
	}
}

int main() {
	Vector a, b, p;

	cin >> a.x >> a.y;
	cin >> b.x >> b.y;
	cin >> p.x >> p.y;

	std::cout << getSegmentDistance(a, b, p);

	return 0;
}

0 0
5 0
1 1

1